Métricas de evaluación

Teniendo en cuenta que las imágenes resultantes del pipeline del procesamiento son binarias, en particular, una configuración de regiones conexas de píxeles negros sobre fondo blanco, es importante que la métrica a utilizar para el matcheo capture la diferencia entre estas estructuras. Teniendo esto en cuenta estudiamos distintas las siguientes métricas:

Interseccion sobre unión (IoU)

Partiendo de la premisa de que lo que estamos comparando son imágenes del mismo tamaño, tiene sentido pensar que una medida de similaridad entre dos imágenes es el área de superposicion de las estructuras que corresponden al patrón de bigotes sobre la suma total de estructuras de las dos imágenes. De esta forma podemos plantear la métrica de la siguiente manera:

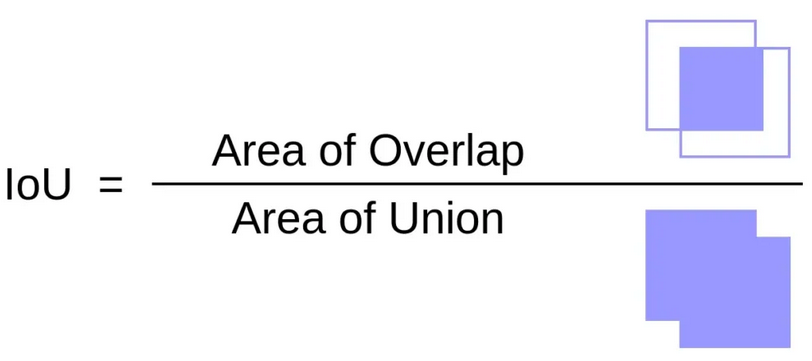
Esta métrica toma valores entre 0 y 1, donde cuanto mayor sea su valor, mayor es la similitd de los conjuntos. En nuestro caso, es de esperar que en fotos de bigotes pertenecientes a un mismo gato, su valor de \(IoU\) sea más alto que al evaluar gatos distintos.

A continuación, en la figura 2 podemos ver un ejemplo de esto, donde se observa la superposición de dos imágenes binarizadas de folículos de un mismo gato, tomadas de fotos distintas. Notar que la intersección de las estructuras, resaltada en color negro, corresponde a un 53% de la suma total de las estructuras de los bigotes. Por otro lado, en la figura 3 se muestra el caso análogo, pero esta vez con imágenes pertenecientes a gatos distintos. Como es de esperar, la superposición de las estructuras es menor en proporción en comparación con el caso anterior, con un 17% de superposición.

Error cuadratico medio (mse)

Otra forma de interpretar las imágenes a comparar es que, en caso de perteneces al mismo gato, una imagen será una deformación elástica de la otra, y en caso de que no se trate del msimo gato, no habrá una transformación elastica que pueda llevar un patrón en el otro. Teniendo esto en mente, una forma válida de medir la distorsión entre dos imágenes es calcular el error cuadrático medio entre las mismas.

Donde \(A\) y \(B\) son imagenes de tamaño \(N \times M\).

En nuestro caso, esperaríamos que cuando se tarta de patrones de bigotes pertenecientes al msimo gato la medida de \(mse\) tendiera a cero mientras que para patrones de gatos distintos, el valor crezca.

Chamfer distance (con variante)

La distancia de Chamfer es una medida utilizada para evaluar la similitud entre dos conjuntos de puntos. Esta métrica es especialmente útil para comparar formas y contornos. Para nuestras imágenes comparamos los conjuntos de puntos negros, es decir, utilizamos todos los píxeles correspondeintes a las regiones conexas del patrón de bigotes para el cálculo. El cálculo de la distancia de Chamfer sigue estos pasos:

1. Búsqueda de Vecino Más Cercano: Para cada punto en el primer conjunto, encuentra el punto más cercano en el segundo conjunto.
2. Cálculo de Distancia: Mide la distancia entre cada par de vecinos más cercanos.
3. Condensar en un único valor: Calcula la mediana de estas distancias (promedio en el algoritmo original)
4. Medición Bidireccional: Repite el proceso invirtiendo los roles de los conjuntos, luego se promedian estos dos resultados.

Tomamos la decisión de condensar las distancias aplicando la mediana en vez del promedio, para que la métrica fuera menos sensible a outliers, e inspirados en lo que se realiza en el artículo científico que utilizamos de referencia del proyecto.

Correlación

Consideramos que la correlación también es una forma válida de medir el grado de semejanza entre los patrones formados por los pixeles negros de los folículos, ya que es relativamente robusta ante pequeñas defromaciones elásticas o traslaciones que no hayan podido ser corregidas durante el preprocesamiento. De esta froma la elegimos como métrica a optimizar a la hora de hacer el registrado en el preprocesamiento y también como valoracion de que tan similares son las imágenes, donde una mayor correlación implica mayor similitúd.

Índice de correspondencias de regiones conexas

Esta métrica fue propuesta por nosotros, consiste en considerar las correspondencias bidireccionales entre las regiones conexas de dos imágenes binarias. Para cada región conexa en una imagen, se identifica la región más cercana en la otra imagen, y se cuenta como una correspondencia válida solo si esta relación es recíproca. El índice final se calcula dividiendo el número de estas correspondencias bidireccionales por el número mínimo de regiones conexas en ambas imágenes, proporcionando así una medida intuitiva y precisa de la similitud estructural entre las dos imágenes.

Análisis de resultados

Una vez tuvimos nuestras imagenes binarias ajustadas procedimos a evaluarlas usando las métricas descritas anteriormente, buscando cuál de ellas logra separar mejor los conjuntos en los que ambas imagenes pertenecen a bigotes del mismo gato de las que no. Para ello tomamos un subconjunto de 24 gatos a modo de entrenamiento, del cual pudimos obtener 100 pares de bigotes correspondientes y 3322 pares de bigotes no correspondientes al mismo individuo.

Aplicamos nuestro pipeline sobre esta base y registramos los valores de las métricas chamfer distance, IoU, mse, correlación y índice de correspondencia para cada comparación, de forma que posteriormente pudieramos graficar sus distribuciones y comportamiento estadístico.

En la siguiente figura presentamos una comparación de los histogramas (figura 4) y boxplots (figura 5) de todas las métricas estudiadas.

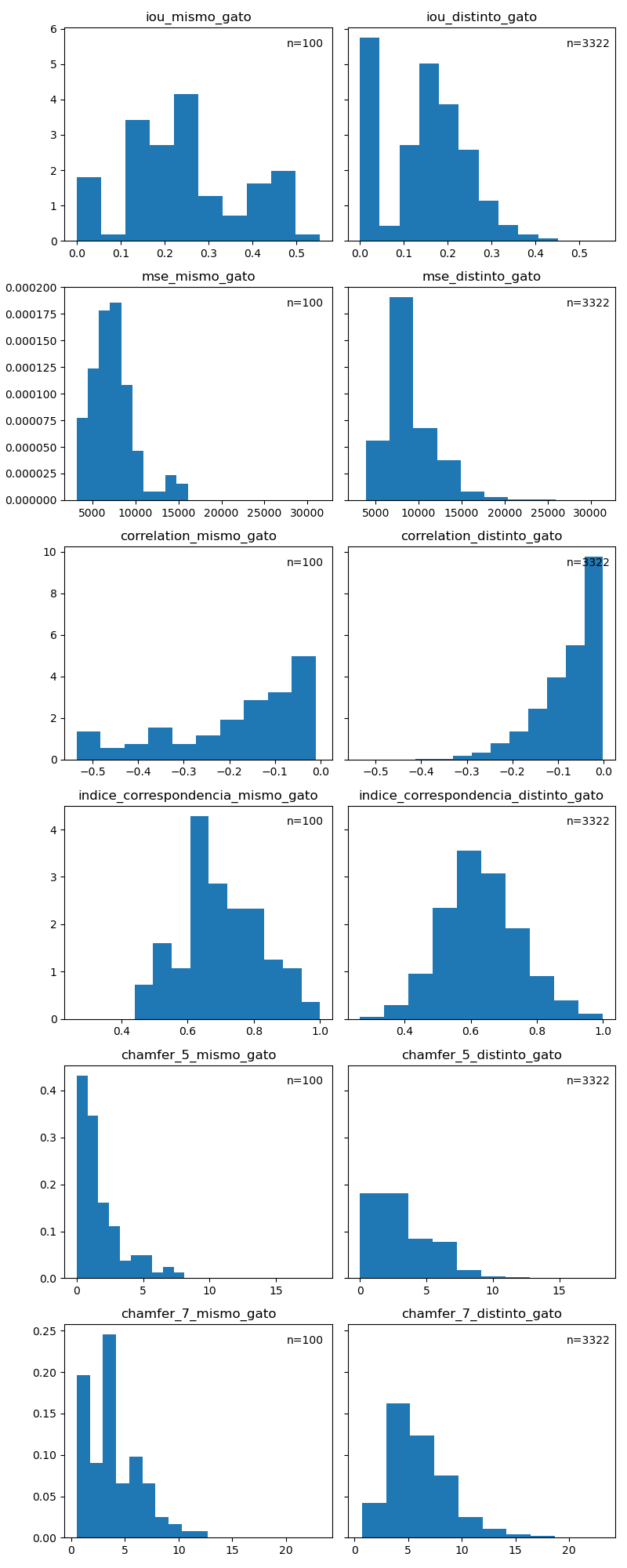
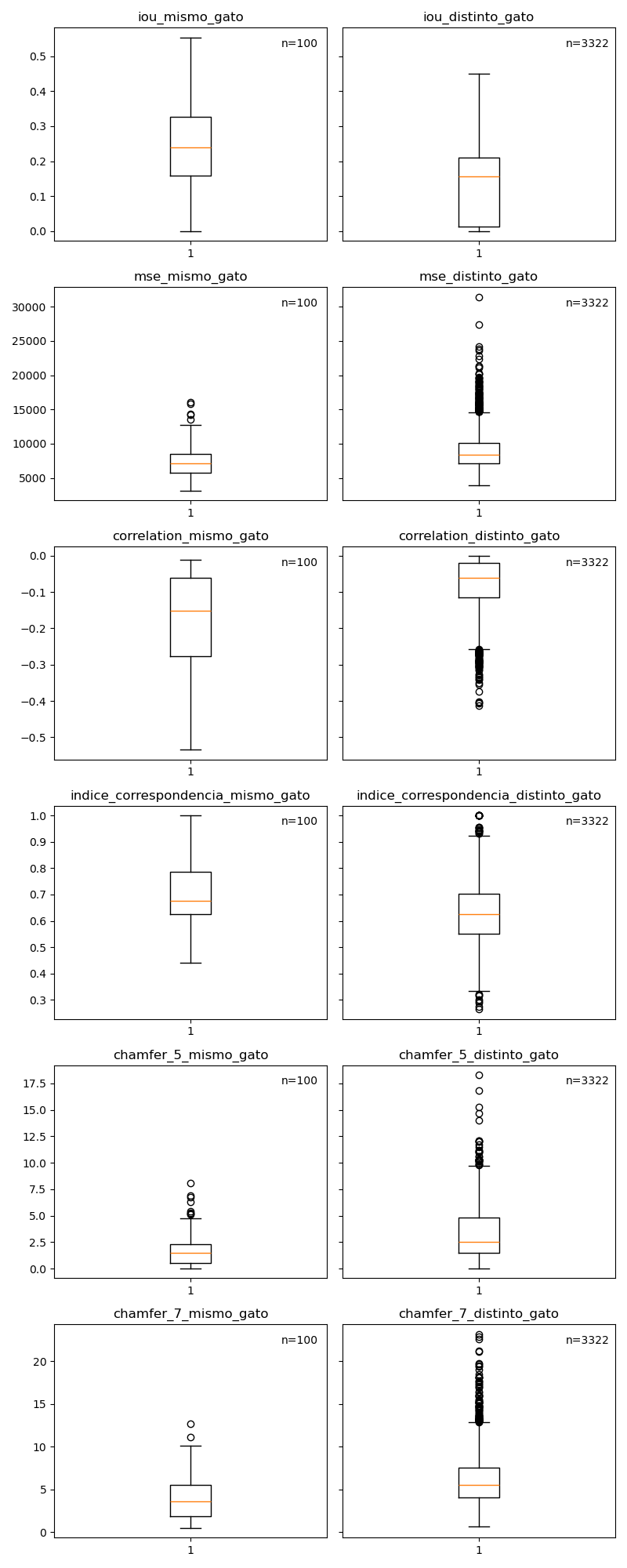
Si observamos los histogrmas de IoU para bigotes de gatos iguales y distintos podemos ver que si bien tienen una tendencia similar, cuando los gatos no son iguales el porcentaje de intersección sobre unión de las estructuras no supera del 40%. Dicho esto y teniendo en cuenta que se presentaron varios outliers, la métrica no se comportó de forma claramente discriminatoria como esperábamos originalmente.

En el caso de mse vemos que para gatos iguales el comportamiento fue lo esperado, con valores que se acumulan por debajo del 10000. Dicho esto, vemos que para gatos distintos, si bien hay muchos más outliers que hacen aumentar la media, esta no varía mucho ya que también hay muchos casos en que el mse esta por debajo del 10000, por lo que tampoco la consideramos como una métrica confiable para hacer una discriminación.

Al analizar la distribución de los valores obtenidos para la métrica correlación vemos que tiene una tendencia algo similar a la de IoU en valor absoluto, pero con un comportamiento mucho más marcado, donde para gatos distintos la correlación entre las imágenes tiende a cero. Entendemos que esto se debe a que al medir la correlación entre los píxeles de dos imágenes se está tomando la medida de superposición de sus estructuras, lo que también capta IoU. De esta forma, es de esperar que tampoco se lograra marcar un umbral claro que separara ambas distribuciones de forma satisfactoria.

Por último analizamos el comportamiento de la medida de chamfer distance en dos de sus variantes: usando el cuantil 0.5 (mediana) para tomar como valor representativo de las distancias entre píxeles de las dos imágenes, y usando el cuantil 0.7. En este caso podemos notar una tendencia más marcada, con valores que acumulan cerca de cero cuando los bigotes pertenecen al mismo gato en comparación a cuando se trata de gatos distintos, siendo que en este caso los valores se distribuyen en un rango mucho mayor.